"The value of `(x^2(yz)^2)/((xz)^2y^2)(y^2(xz)^2)/((xy)^2z^2)(z^2(xy)^2)/((yz)^2x^2)`is`1`(b) 0 (c) 1 (d) None of these"This integral of a function along a curve C is often written in abbreviated form as ∫ C f ( x, y) d s Example 1621 Compute ∫ C y e x d s where C is the line segment from ( 1, 2) to ( 4, 7) We write the line segment as a vector function r = 1, 2 t 3, 5 , 0 ≤ tThe sphere x2 y 2 z = 16 and outside the cylinder x2 y = 4 Solution The sphere x2 y2 z2 = 16 intersects the xyplane along the circle with equation x 2 y = 16 Since the solid is symmetric about the xyplane, we may compute its total volume as twice the volume of the part that lies above the xyplane, and this
The Divergence Theorem
X^2+y^2+z^2=16
X^2+y^2+z^2=16-Guillemin and Pollack Chapter 1, Section 4, Problem 5I did this to better visualise a problem for a Differential Geometry course at the University of MichigExample 1671 Suppose a thin object occupies the upper hemisphere of $x^2y^2z^2=1$ and has density $\sigma(x,y,z)=z$ Find the mass and center of mass of the




Factorize 9 X Y 2 16 X 2y 2 Brainly In
Fx(x,y) = sin(xy)xcos(xy) and fy(x,y) = xcos(xy) and fz = cosz At (2,2,0), fx(2,−2,0) = sin0 2cos0 = 2 and fy(2,−2) = 2cos0 = 2 and fz(2,2,0) = 1 Therefore the tangent plane is 0 = 2(x−2)2(y 2)−z = 2x2y −z 2 Test the function f(x,y) = x4 y3 32x − 27y for local maxima, minima and saddle points (18) Solution Find theFigure 2 Part of the region S bounded by x2z2 = a2 and x2 y2 = a2 for x ≥ 0 Note that the projection of region S1 on the y − z plane, call it R is a a square 0 ≤ y ≤ a, 0 ≤ z ≤ a We break Experts are tested by Chegg as specialists in their subject area We review their content and use your feedback to keep the quality high Transcribed image text Find the volume of the solid inside the sphere x^2 y^2 z^2 = 16, above the
The lower bound z = x 2 y 2 z = x 2 y 2 is the upper half of a cone and the upper bound z = 18 − x 2 − y 2 z = 18 − x 2 − y 2 is the upper half of a sphere Therefore, we have 0 ≤ ρ ≤ 18, 0 ≤ ρ ≤ 18, which is 0 ≤ ρ ≤ 3 2 0 ≤ ρ ≤ 3 2 For the ranges of φ, φ, weDivide yz, the coefficient of the x term, by 2 to get \frac{yz}{2} Then add the square of \frac{yz}{2} to both sides of the equation This step makes the4 Find the volume and centroid of the solid Ethat lies above the cone z= p x2 y2 and below the sphere x 2y z2 = 1, using cylindrical or spherical coordinates, whichever seems more appropriate Recall that the centroid is the center of mass of the solid
x2 y2 = 16 Note that we can rewrite this equation as (x −0)2 (y −0)2 = 42 This is in the standard form (x −h)2 (y −k)2 = r2 of a circle with centre (h,k) = (0,0) and radius r = 4 So this is a circle of radius 4 centred at the origin graph {x^2y^2 = 16 10, 10, 5, 5} Answer link§162 DOUBLE INTEGRALS OVER GENERAL REGIONS Z 1x2 0 f(x,y,z) dz dy dx 276 §164 TRIPLE INTEGRALS Extra Example Set up the integral to find the mass of the region E bounded by the parabolic cylinder z = 1 y2 and the planes x z = 1, x = 0, and z = 0, given theConstraint 2g(x,y,z)= x y2z2=4 Using Lagrange multipliers, solve ∇f= λ ∇g and g=4 This gives Continued •2(x3)=2xλ (12) •2(y1)=2yλ (13) •2(z1)=2zλ (14) •x 2y z2=4 (15) •The simplest way to solve these equations is to solve for x, y, and z



Surface Area
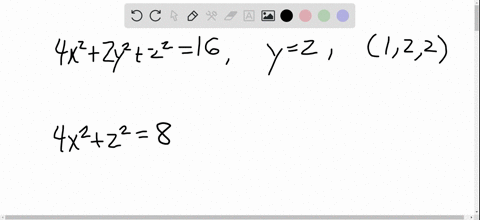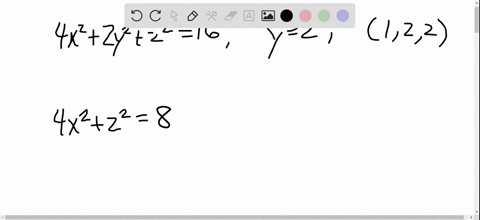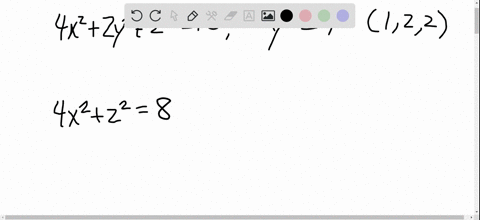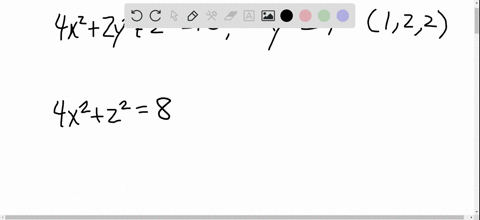



Solved The Ellipsoid 4 X 2 2 Y 2 Z 2 16 Intersects The Plane Y 2 In An Ellipse Find Parametric Equations For The Tangent Line To This Ellipse At The Point 1 2 2
(Definition 2 in Section 162);The definition of a double integral (Definition 5 in Section 151) To evaluate the surface integral in Equation 1, we approximate the patch area ∆S ij by the area of an approximating parallelogram in the tangent plane , 11 ( , , ) lim ( ) mn ij ij mn S ij f x y z dS f P S ofSolution to Problem Set #9 1 Find the area of the following surface (a) (15 pts) The part of the paraboloid z = 9 ¡ x2 ¡ y2 that lies above the x¡y plane ±4 ±2 0 2 4 x ±4 ±2 0 2 4 y ±4 ±2 0 2 4 Solution The part of the paraboloid z = 9¡x2 ¡y2 that lies above the x¡y plane must satisfy z = 9¡x2 ¡y2 ‚ 0 Thus x2 y2 • 9 WeStack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange




Surfaces Part 2



Solved Use Cylindrical Coordinates Evaluate Iiint E X Y Dv Where E Is The Solid That Lies Between The Cylinders X 2 Y 2 1 And X 2 Y 2 16
(x y) dV where Eis the solid that lies between the cylinders x2 y2 = 1 and x 2 y = 16, above the xyplane, and below the plane z= y 4 Hint Use cylindrical coordinates coordinates2 0 hx;y;z4i(r r ˆ)dˆd = Z 2ˇ 0 Z p 2 0 ˆ 2 p 2 ˆ5 8 dˆd = 2ˇ Z 2 0 ˆ2 2 p 2 ˆ5 8 dˆ = 1 3 1 6 = 1 6 1784 Use Stokes' Theorem to evaluate ZZ S curlFdS when F(x;y;z) = x2y3zi sin(xyz)j xyzk, and Sis the part of the cone y2 = x2 z2 that lies between the planes y= 0 and y= 3, oriented in the direction of the positive yaxisSo we have to solve z z z in terms of x x x and y y y x 2 y 2 z 2 = 16 → z 2 = 16 − x 2 − y 2 → z = ± 16 − x 2 − y 2 x^2y^2z^2=16 \rightarrow z^2 = 16 x^2 y^2 \rightarrow z= \pm\sqrt {16 x^2 y^2 } x 2 y 2 z 2 = 16 → z 2 = 16 − x 2 − y 2 → z




If Z X Iy And X 2 Y 2 16 Then The Range Of Abs Abs X Abs Y Is Youtube



The Divergence Theorem
Z= ˆcos˚ It follows that x2 y2 = ˆ2 sin2 ˚ If we de ne the angle to have the same meaning as in polar coordinates, then we have x= ˆsin˚cos ;;˚) Example To convert the point (x;y;z) = (1;R = {(x,y,z) x2 y2 6 22, x2 y2 6 z 6 4} Solution 2 x 2 y 4 z z = x y The symmetry of the region implies x = 0 and y = 0 (We verify this result later on) We only need to compute z Since z = 1 V ZZZ R z dv, we start computing the total volume V We use cylindrical coordinates V = Z 2π 0 Z 0 Z 4 r2 dz rdr dθ = 2π Z 0 z 4 r2 rdr




Using Geometry Calculate The Volume Of The Solid Under Z Sqrt 16 X 2 Y 2 And Over The Circular Disk X 2 Y 2 Leq 16 Study Com




Consider The Region Above The Xy Plane Inside The Sphere X 2 Y 2 Z 2 16 And Outside The Cylinder X 2 Y 2 4 A Sketch The Region By Hand Or With The
The intersection of z= 4 2x 22y and xyplane is 0 = 4 x2 y;ie x2 y = 4 In polar coordinates, z= 4 x2 y 2is z= 4 rSo, the volume is Z Z 4 x2 y2dxdy = Z 2ˇ 0 Z 2 0 4 r2 rdrd = 2ˇ Z 2 0 4r r3 2 dr= 2ˇ 2r2 1 4 r4 = 2ˇ(8 4) = 8ˇ 3 Evaluate Z Z Z T y2dxdydz where T is the tetrahedron in the rst constant bounded by the coordinate planes and1i th1;0;0i 11 Consider the paraboloid z = x2 y2 (a) Compute equations for the traces in the z = 0, z = 1, z = 2, and z = 3Example Find the volume of the solid region above the cone z2 = 3(x2 y2) (z ≥ 0) and below the sphere x 2 y 2 z 2 = 4 Soln The sphere x 2 y 2 z 2 = 4 in spherical coordinates is ρ = 2




If A X 2 Y 2 16 And B 9x 2 25y 2 225 Find N A Intersection B Brainly In



Solved Find The Surface Area Of The Part Of The Hemisphere Chegg Com
Math 2263 Quiz 10 26 April, 12 Name 1 Evaluate RR S zdS, where S is the part of the plane 2x 2y z = 4 that lies in the rst octant Answer The x, y In Mathematica tongue x^2 y^2 = 1 is pronounced as x^2 y^2 == 1 x^2y^2=1 It is a hyperbola, WolframAlpha is verry helpfull for first findings, The Documentation Center (hit F1) is helpfull as well, see Function Visualization, Plot3Dx^2 y^2 == 1, {x, 5, 5}, {y, 5, 5} ContourPlot3Dx^2 y^2 == 1, {x, 5, 5}, {y, 5, 5}, {z, 5, 5}X 2 / 2 y 2 /b 2 is 2 y 2 /b 2 is 2 y 2 /b 2 z 2 /c 2 = 0 is a cone Example Name the following quadric Solution Notice that the trace on the xyplane is x 2 y 2 = 1 is a hyperbola and on the xzplane is x 2



Let The Tangents Drawn To The Circle X2 Y2 16 From The



Solved Consider The Solid That Is Bounded By The Cone Z 3 X 2 3 Y 2 And Above By The Sphere X 2 Y 2 Z 2 16 Set Up Only The Appropriate Tripl Course Hero
F(x, y, z) = –y2 i x j z2 k C is the curve of intersection of the plane y z = 2 and the cylinder x2 2 y = 1 (Orient C to be counterclockwise when viewed from above) could be evaluated directly, however, it's easier to use Stokes' Theorem C ∫Fr⋅d Example 1 C ∫Fr⋅dDe ned by z= x 2 y2 and x 2y2 z2 = 7 at the point ( 1;1;2) Hint Think about the geometry of the gradient vectors You don't have to parametrize the curve to do this problem Solution The surface z= x2 y2 can be written as the level surface F(x;y;z) = x 2 y z= 0; In terms of our new function the surface is then given by the equation f (x,y,z) =0 f ( x, y, z) = 0 Now, recall that ∇f ∇ f will be orthogonal (or normal) to the surface given by f (x,y,z) =0 f ( x, y, z) = 0 This means that we have a normal vector to the surface The only potential problem is that it might not be a unit normal vector




Ex 6 3 13 Find Points On X2 9 Y2 16 1 At Which Tangents



How To Fill A Solid Defined By X 2 Y 2 9 Z 16 X 2 Y 2 And Z 0 Using Pgfplots Tex Latex Stack Exchange
Y= ˆsin˚sin We de ne the spherical coordinates of (x;y;z) to be (ˆ;' (t) = h1;Verify Stokes' Theorem for the field F = hx2,2x,z2i on the ellipse S = {(x,y,z) 4x2 y2 6 4, z = 0} Solution We compute both sides in I C F·dr = ZZ S (∇×F)·n dσ S x y z C 2 1 1 2 We start computing the circulation integral on the ellipse x2 y2 22 = 1 We need to choose a counterclockwise parametrization, hence the normal to




Tim X Y Z X 2 Y 3 Z 4 Va X 2 Y 2 X 2 116 Cau Hỏi 1935 Hoidap247 Com



What Is The Minimum Value Of Sqrt 4 Y 2 Sqrt X 2 2 Y 2 2 Sqrt X 5 2 4 Quora
The cone z = sqrt(x^2 y^2) can be drawn as follows In cylindrical coordinates, the equation of the top half of the cone becomes z = r We draw this from r = 0 to 1, since we will later look at this cone with a sphere of radius 1 Example 4 Find the volume of the region that lies inside \(z = {x^2} {y^2}\) and below the plane \(z = 16\) Show Solution Let's start this example off with a quick sketch of the region Now, in this case the standard formula is not going to work The formula3 O plot3d({sqrt(9x^2), sqrt(9y^2)},x=33,y=33);




Evaluate The Volume Of The Solid Bounded By Z 8 X 2 Y 2 Z X 2 Y 2 X 1 Y Sqrt 3 X Y 0 Mathematics Stack Exchange




Find The Following Products Z 3 4 Z 4 3 Ii X 2 4 X 2 9 Y 2 12 Y 2 6 Iv X 2 4 X 2 9 P 2 16 P 2 1 4
Ellipsoids are the graphs of equations of the form ax 2 by 2 cz 2 = p 2, where a, b, and c are all positive In particular, a sphere is a very special ellipsoid for which a, b, and c are all equal Plot the graph of x 2 y 2 z 2 = 4 in your worksheet in Cartesian coordinates Then choose different coefficients in the equation, and plot aThe boundary is where x2 y2 z2 = 25 and z= 4 Substituting z= 4 into the rst Substituting z= 4 into the rst equation, we can also describe the boundary as where x 2 y 2 = 9 and z= 4And so the gradient of Fis rF(x;y;z) = h2x;2y;



Link Aps Org




Resoudre X 16 0 Youtube
The sphere x2 y2 z2 = 4 and the coordinate planes using Rectangular Coordinates G xy⋅⋅z V ⌠ ⎮ ⌡ d x y z 0 2 x 0 4x−2 y 0 4x−2−y2 xy⋅⋅z z ⌠ ⎮ ⌡ d ⌠ ⎮ ⌡ d ⌠ ⎮ ⌡ d Page 10 of 18 Yes, it is correct The same result can be obtained, by rotating around the z axis, through an agle of π 2, the graph of x ( z) = 16 − z S = π 2 ∫ 0 16 x ( z) 1 ( x ′ ( z)) 2 d z = π 24 ( 65 65 − 1) Share Follow this answer to receive notifications answered Sep 19 '17 at 1452 Robert Z Robert Z 135k 12Z=x^2y^2 WolframAlpha Natural Language Math Input Extended Keyboard




Find And Sketch The Domain Of The Function F X Y Z Ln 16 4x 2 4y 2 Z 2 Youtube




Factorise 25 2x Y 2 16 X Y 2 Brainly In
Solution We can optimize the distance x 2 y 2 z 2 by optimizing the function f (x, y, z) = x 2 y 2 z 2, which has a simpler derivative We let g (x, y, z) = xy z be the plane constraint, and h (x, y, z) = x 2 y 2 be the cylinder constraint We see thatIn the twodimensional coordinate plane, the equation x 2 y 2 = 9 x 2 y 2 = 9 describes a circle centered at the origin with radius 3 3 In threedimensional space, this same equation represents a surface Imagine copies of a circle stacked on top of each other centered on the zaxis (Figure 275), forming a hollow tube4) to spherical coordinates, we rst compute ˆ= p x2 y2 z2 = q




ダウンロード済み Grafica De X 2 Y 2 16 4795 Grafica De La Ecuacion X 2 Y 2 16
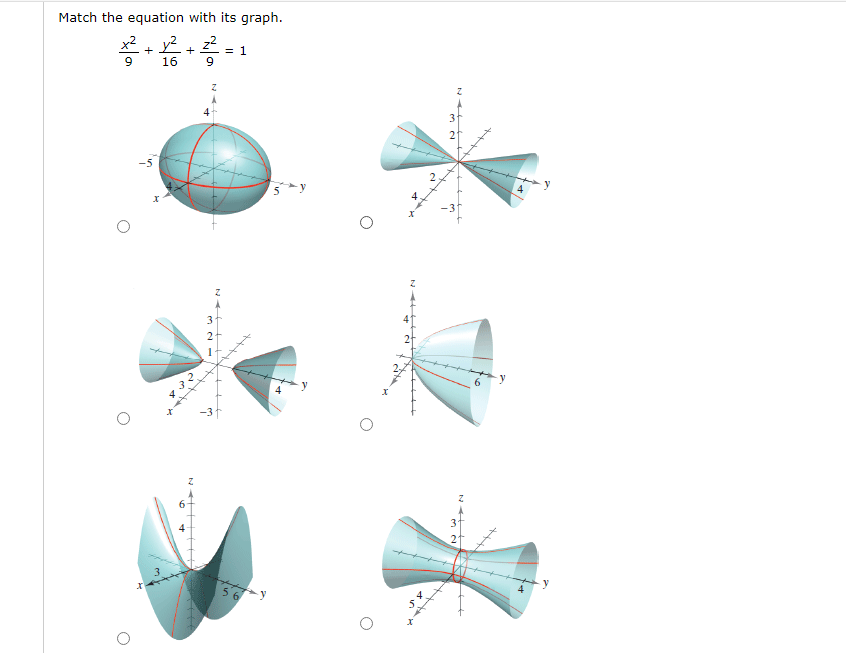



Solved Match The Equation With Its Graph X2 Y2 22 1 9 Chegg Com
4(x 21)2 (y 5) 16(z 1)2 = 37 This is a hyperboloid of 1 sheet which has been shifted Speci cally, its central axis is parallel to the xaxis In fact, the equation of its central axis is!Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, musicAlgebra Graph 4x^2y^2=16 4x2 y2 = 16 4 x 2 y 2 = 16 Find the standard form of the ellipse Tap for more steps Divide each term by 16 16 to make the right side equal to one 4 x 2 16 y 2 16 = 16 16 4 x 2 16 y 2 16 = 16 16 Simplify each term in




Upper Left Lower Left Panel 3 And Upper Right Panels Plots Of D Download Scientific Diagram




Surface Area Of Sphere X 2 Y 2 Z 2 16z Within Paraboloid Z X 2 Y 2 Mathematics Stack Exchange
Answer (1 of 5) It's the equation of sphere The general equation of sphere looks like (xx_0)^2(yy_0)^2(zz_0)^2=a^2 Where (x_0,y_0,z_0) is the centre of the circle and a is the radious of the circle It's graph looks like Credits This 3D Graph is created @ code graphing calculatorCalculus questions and answers Evaluate tripleintegral_B e (x^2 y^2 z^2)^3/2 where B is the ball B = { (x, y, z) x^2 y^2 z^2 lessthanorequalto 16} SOLUTION Since the boundary of B is a sphere, we use spherical coordinates B = { (rho, theta, phi) 0 lessthanorequalto rho lessthanorequalto 4,0 lessthanorequalto theta lessthanorequalto 2 pi,0 lessthanorequalto phi4 Find the mass of a ball B given by x2 y2 z2 ≤ a2 if the density at any point is proportional to its distance from the zaxis (use cylindrical coordinates) Solution Since the density is proportional to the distance from the zaxis, the density function is f(x,y,z) = k p x2 y2 The plane region D is a disk with radius a So E 0 ≤




Mathmod Klein Bottle By Torolf Sauermann Http Www Evolution Of Genius De Gallery Default4 Htm Facebook




Solve X Y 18 Y Z 12 Z X 16
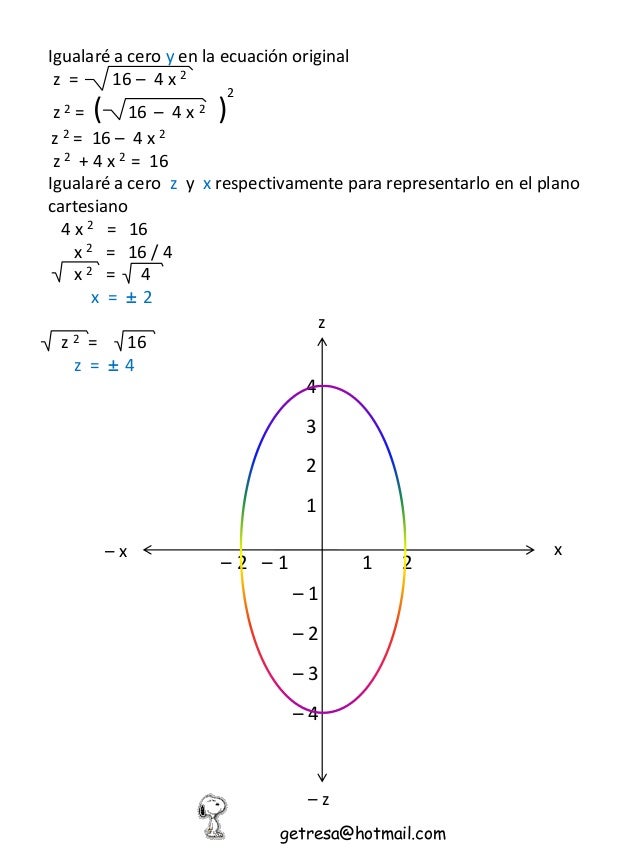
Polar Coordinates Evaluate the integral ZZ D e x2 y2 dA, where Dis the region bounded by the semicircle x= p 4 y2 and the yaxis ZZ D e x2 y2 dA= Z 2 r=0 Z ˇ=2 = ˇ=2 er2rdrd = ˇ Z 2 r=0 rer2 dr ˇ 2 er2j2 0 = ˇ 2 (e4 1) Find the volume of the solid inside the sphere x 2 y2 z = 16 and outside the cylinder x2 y2 = 4 Express this as twice the integral of the function z=X2 − y2 = 16 x 2 y 2 = 16 Find the standard form of the hyperbola Tap for more steps Divide each term by 16 16 to make the right side equal to one x 2 16 − y 2 16 = 16 16 x 2 16 y 2 16 = 16 16 Simplify each term in the equation in order to set the right side equal to 1 1 See below Considering the variables x,y,z defining RR^3, this geometrical object is a surface such that for any x obeys y^2z^2= 16 so it is a cylindrical surface centered at the x axis having a circle with radius 4 as transversal cross section
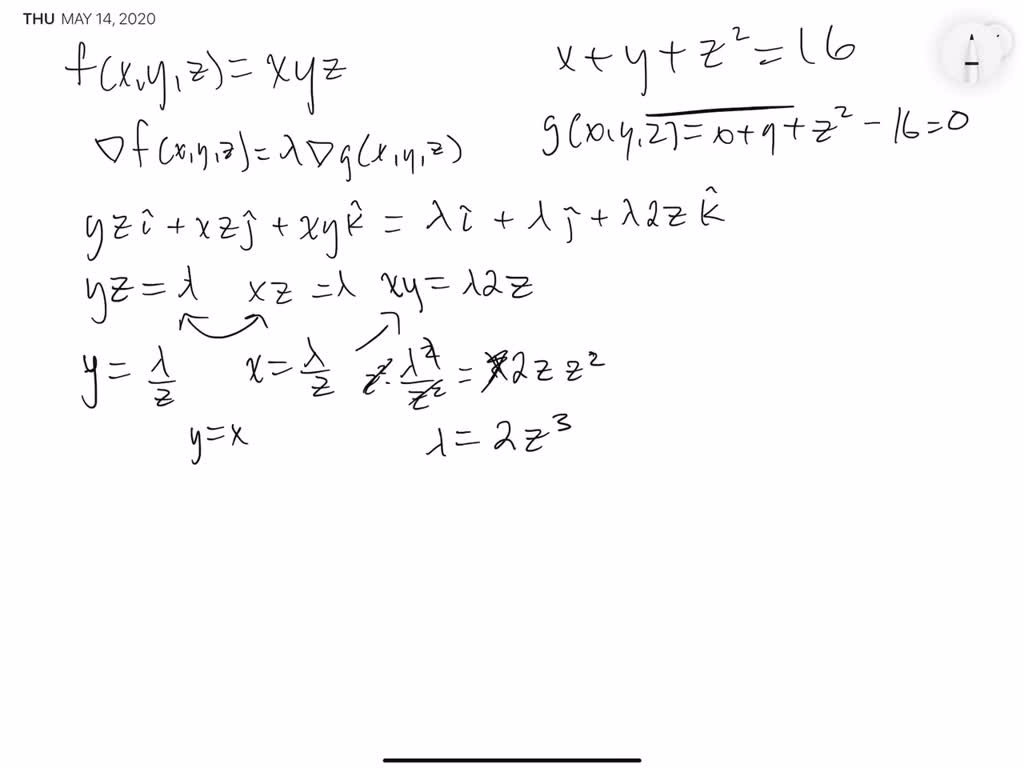



Solved Maximizing A Product Find The Largest Product The Positive Numbers X Y And Z Can Have If X Y Z 2 16



Surface Area




Factorize 9 X Y 2 16 X 2y 2 Brainly In



If A X Y X2 Y2 25 And B X Y X2 16y2 1




O Ab X 2x 12y 2y 12z 2z




Evaluate1 F O Zy 2 Ds S 2 16 X2 Y2 1 Itprospt




Graph The Cylinder X 2 Y 2 16 And The Sphere X 2 Y 2 Z 2 49 Together Using Maple And Find The Volume Outside The Cylinder And Inside The Sphere Study Com



1



Math Drexel Edu



1 Factorise The Following Using Identities A 9x 2 24x 16 B 4x 2 Y 2 4xyz Z 2 E X 2 2 Frac 1 X 2 D X 4 10x 2 Y 2 25y 4 E 64a 2 25k2 Snapsolve



Graficar Calcular Superficie




Use Cylindrical Coordinates To Find The Volume Of The Solid Solid Inside Both X2 Y2 Z2 16 Homeworklib




Use Polar Coordinates To Find The Volume Of The Given Solid Inside The Sphere X2 Y2 Z2 16 And Outside The Cylinder X2 Y2 9 Study Com



12 6 Cylinders And Quadric Surfaces
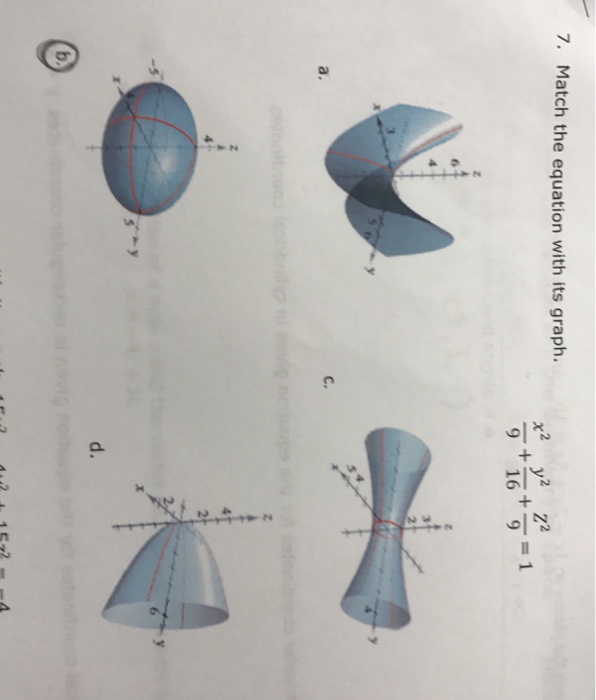



Solved Match The Equation With Its Graph X 2 9 Y 2 16 Chegg Com




Solved Name The Surfaces 4x 2 Y 2 16 Z 2 2 100 Chegg Com




Nk6875td23hg8m




Left Begin Array L 25 X 2 16 Y 2 4 Scholr




Elliptic Paraboloid X 2 Y 2 Z 2 0 Download Scientific Diagram




Rd Sharma Solutions For Class 8 Chapter 7 Factorization Exercise 7 6 Free Pdf



1



2x 3y 2z 16 X 2y 2z 6 5x Y 3z 25 Gauthmath




Describe Sketch And Name These Cylinders And Quadric Surfaces In R 3 A 4 X 2 16 Y 2 Z 2 16 B X 2 4 Y 2 4 Z 2 0 C X 2 Y 3 Z 12 D Y 2 Z 2 9 Study Com




Rise X 2 9 Y 2 16 Z 2 12 X Y 24 Y Z 16 X Z X 2 Y 2 8 Z 2 2 Sqrt 2 X Y 4 Sqrt 2 Y Z 8 X
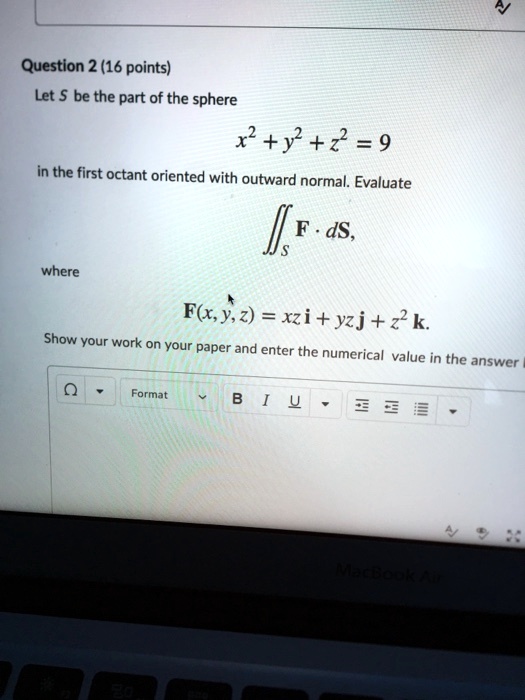



Question 2 16 Points Let Be The Part Of The Sphere Itprospt




If X X 1 X 2 Represents




Oneclass Find The Volume Of The Solid Enclosed By The Paraboloids Z 16 X2 Y2 And Z 2 16 X



Solve The Following Systems Of Linear Equations By Cramer S Rule I 5x 2y 16 0 X 3y 7 0 Ii 3 X 2y 12 2 X 3y 13 Sarthaks Econnect Largest Online Education Community



6 7 Maxima Minima Problems Mathematics Libretexts



Arxiv Org



Y 2 Z 2 16 Is This Represents A Circle In 3 Dimensional Space Or 2 Dimensional Space Socratic




The Paraboloid X 2 Y 2 16 Z Is Intersected By The Ellipsoid X 2 4 Download Scientific Diagram




Contiune On 16 7 Triple Integrals Figure 1 Ef X Y Z Dv




Graph X 2 Y 2 16 What Are Its Lines Of Symmetry Brainly Com




Solution Evaluate X 2 Y 2 Dv Over The Region In The First Octant Bounded By X 2 Y 2 2



Volume Of Figure Between X 2 Y 2 Z 2 16 And X 2 Y 2 6z If Z Geq 0 Mathematics Stack Exchange




Solved The Graph Shows The Ellipsoid X 2 4y 2 Z 2 16 Use The Graph To Determine The Equation Of The




How To Find And Count The Points That Are Elements Of X Y In Mathbb Z 2 X 2 Y 2 Le16 Wedge Y Gt X Newbedev




Ex 6 3 13 Find Points On X2 9 Y2 16 1 At Which Tangents




Graphing 3d Graphing X 2 Y 2 Z 2 Intro To Graphing 3d Youtube



Animated Algebraic Surfaces




Solved Find The Volume Of The Solid Inside The Sphere X 2 Chegg Com




The Ellipsoid 4x 2 2y 2 Z 2 16 15 Pages Summary In Google Sheet 5mb Updated Eli Study For Exams




Answered 9 M A Y Z Xyz Xyz P 2 1 1 U Bartleby




Volume Between Sphere And Cone Uconn Mathematics Maker Space
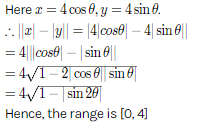



If Z X Iy And X 2 Y 2 16 Then Range Of X Y A 0 4 B 0 2 C 2 Askiitians



1
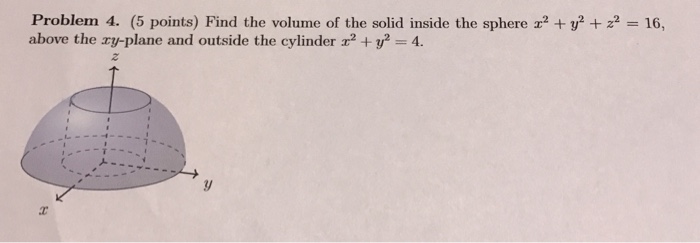



Solved Find The Volume Of The Solid Inside The Sphere X 2 Chegg Com
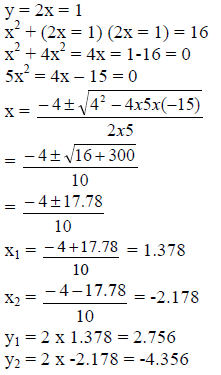



Solve The Following Simultaneous Equations X Sup 2 Sup Y Sup 2 Sup 16 Y 2x 1




Misc 18 Mcq Area Of Circle X2 Y2 16 Exterior To Parabola




Systems Engineering And Analysis Ppt Download
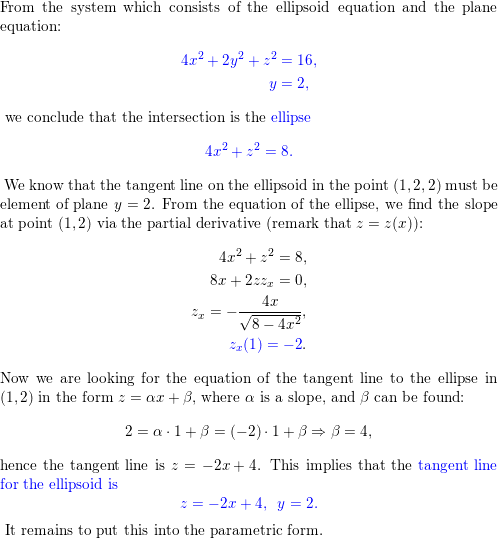



The Ellipsoid 4x 2 2y 2 Z 2 16 Intersects The Plan Quizlet




Notes Up To Ch7 Sec3




Solved The Ellipsoid 4 X 2 2 Y 2 Z 2 16 Intersects The Plane Y 2 In An Ellipse Find Parametric Equations For The Tangent Line To This Ellipse At The Point 1 2 2



Solved Determine The Interaction Of The Line Of Intersection Of The Planes X Y Z 1 And 3x Y Z 3 With The Line Of Intersection Of The Pl Course Hero
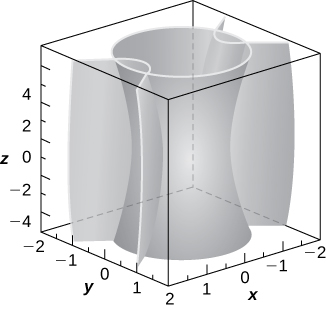



12 6e Exercises For Section 12 6 Mathematics Libretexts




Find The Volume Bounded By 4z 16 X 2 Y 2 And The Plane Z 0 Using Double Integral Mathematics Stack Exchange



Polar Html




1 Point Find The Volume Of The Solid That Lies Within The Sphere X2 2 Z 64 Above The Xy Plane And Outside The Cone Z 8v X2 Y2 1 Point



Math Drexel Edu




1 Point Find The Volume Of The Solid That Lies Within The Sphere X2 Y2 2 16 Above The Xy Plane And Outside The Co Homeworklib




Use Cylindrical Coordinates To Find The Volume Of The Solid Solid Inside Both X2 Y2 Z2 16 Homeworklib



Slice Matlab Function Reference




Misc 18 Mcq Area Of Circle X2 Y2 16 Exterior To Parabola
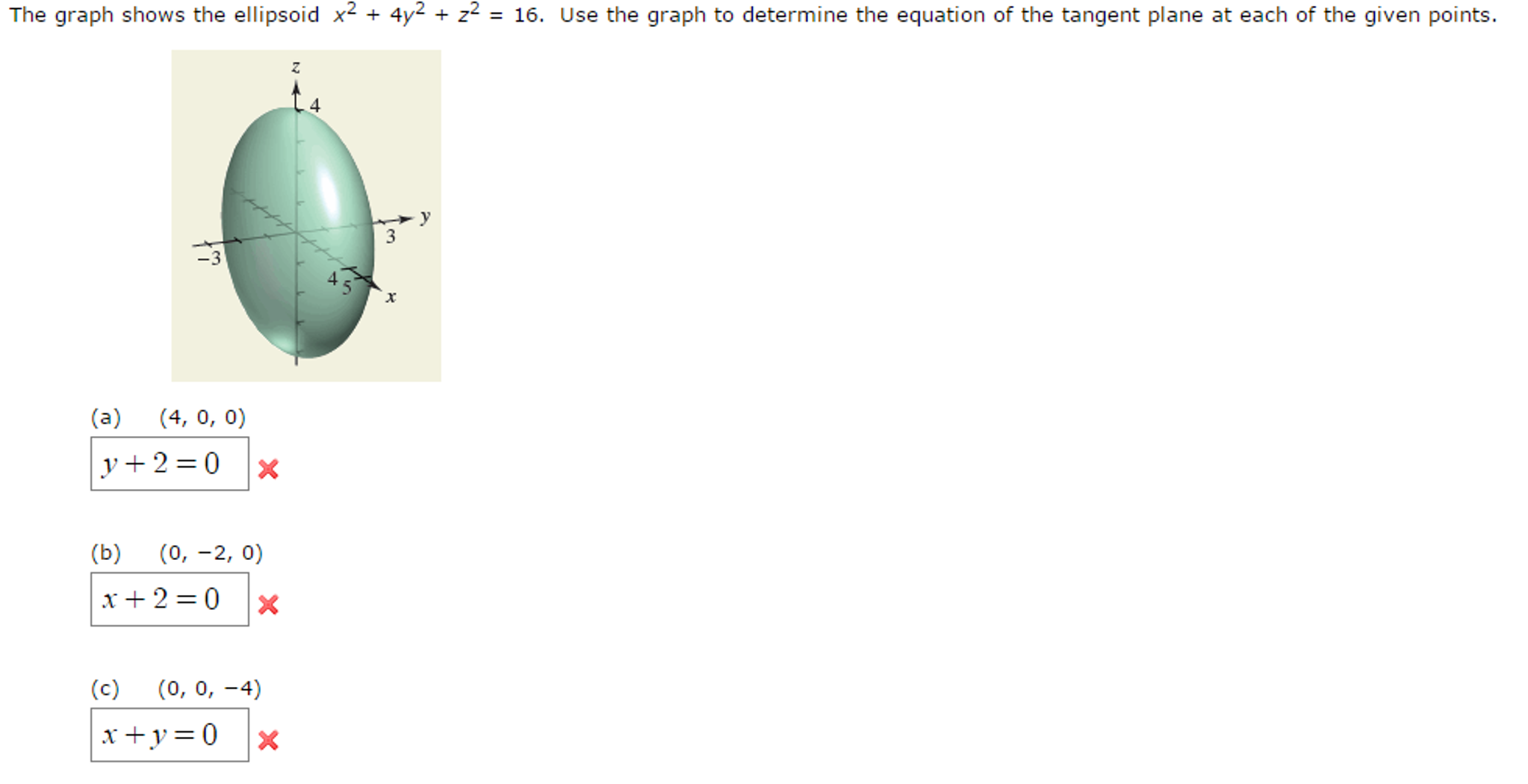



Solved The Graph Shows The Ellipsoid X2 4y2 Z2 16 Chegg Com




Solved We Consider The Hemi Sphere X 2 Y 2 Z 2 16 And Chegg Com



Triple Integrals In Cylindrical And Spherical Coordinates



Math Drexel Edu



Surface Area




Ex 8 1 4 Find Area Bounded By Ellipse X2 16 Y2 9 1



Spherical Coordinates
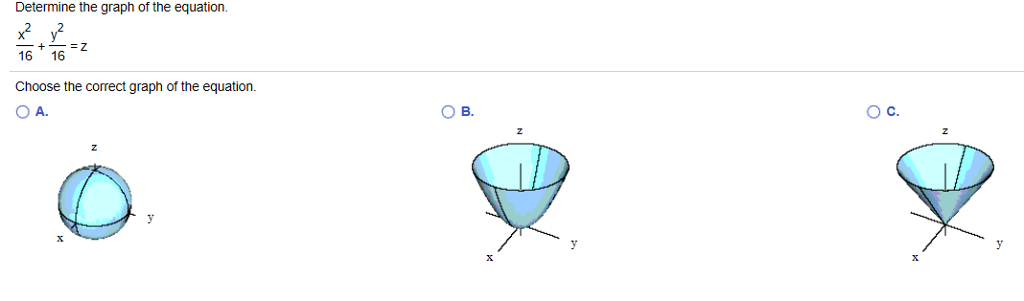



Solved Determine The Graph Of The Equation X 2 16 Y 2 16 Chegg Com




Mh1811 Tutorial 12 Max Min Lag Mult Double Integrals Soln Nanyang Technological University School Studocu




Find The Volume Of The Solid Between The Cylinder X 2 Y 2 4 And The Sphere X 2 Y 2 Z 2 16 Study Com



Sol Purcell Ingles




Solved 3 Match The Equation With The Surface It Defines Chegg Com



0 件のコメント:
コメントを投稿