Partial derivative of ( (5x^2)/ ( (x^2y^2))) full pad » x^2 x^ {\msquare} \log_ {\msquare} \sqrt {\square} \nthroot \msquare {\square} \le \ge It depends on whether we need d/dx or d/dt For d/dt d/dt(ln(x^2y^2)) = 1/(x^2y^2) d/dt(x^2y^2) = 1/(x^2y^2) * (2xdx/dt 2y dy/dt) For d/dx d/dx(ln(x^2y^2)) = 1/(x^2y^2) d/dx(x^2y^2) = 1/(x^2y^2) * (2x 2y dy/dx)Differentiate using the Power Rule which states that d d x x n d d x x n is n x n − 1 n x n 1 where n = 2 n = 2 Since y 2 y 2 is constant with respect to x x, the derivative of y 2 y 2 with respect to x x is 0 0 Combine fractions Tap for more steps Add 2 x 2 x and 0 0 Combine 2 2 and 1 x 2 y 2 1 x 2 y 2

If Logsqrt X 2 Y 2 Tan 1 Y X Then Dy Dx Is
Partial derivative of log(x^2+y^2)
Partial derivative of log(x^2+y^2)- The partial derivative of f with respect to x is fx(x, y, z) = lim h → 0f(x h, y, z) − f(x, y, z) h Similar definitions hold for fy(x, y, z) and fz(x, y, z) By taking partial derivatives of partial derivatives, we can find second partial derivatives of f with respect to z> If u = log (x^2y^2z^2), v maths If u = lo g (x 2 y 2 z 2) Oscillations Redox Reactions Limits and Derivatives Motion in a Plane Mechanical Properties of Fluids class 12 Atoms Chemical Kinetics Moving Charges and Magnetism Microbes in Human Welfare Semiconductor Electronics



What Is The Second Derivative Of Y Log X 2 E X Quora
The partial derivative of a function f with respect to the differently x is variously denoted by f' x,f x, ∂ x f or ∂f/∂x Here ∂ is the symbol of the partial derivative Example Suppose f is a function in x and y then it will be expressed by f(x, y) So, the partial derivative of f with respect to x will be ∂f/∂x keeping y as constantU}{\partial y \partial x} $The partial derivative of a function of multiple variables is the instantaneous rate of change or slope of the function in one of the coordinate directions Computationally, partial differentiation works the same way as singlevariable differentiation with all other variables treated as constant Partial derivatives are ubiquitous throughout equations in fields of higherlevel physics and
Holds, then y is implicitly defined as a function of x The partial derivatives of y with respect to x 1 and x 2, are given by the ratio of the partial derivatives of F, or ∂y ∂x i = − F x i F y i =1,2 To apply the implicit function theorem to find the partial derivative of y with respect to x 1 (for example), first take the total differential of F dF = FPartial derivative of x/ ( (xy)^2) full pad » x^2 x^ {\msquare} \log_ {\msquare} \sqrt {\square} \nthroot \msquare {\square} \le \geIn mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant Partial derivatives are used in vector calculus and differential geometry The partial derivative of a function f {\displaystyle f} with respect to the variable x {\displaystyle x} is variously denoted by f x ′ {\displaystyle f'_{x}}, f x {\displaystyle f_{x}}, ∂ x f {\displaystyle \partial
Sign In Math Central Mathematics is the "Language of the universe (x^2)(y^2)) is equal to (the extra parentheses are just to make our order of operations clear), simply plug in the values you've got for x and y (xy you can have two "partial derivatives" a derivative with respect to "x", and a derivative with respect toJul 14,21 Partial Differential Equation MCQ 2 15 Questions MCQ Test has questions of Mathematics preparation This test is Rated positive by 85% students preparing for MathematicsThis MCQ test is related to Mathematics syllabus, prepared by Mathematics teachersPARTIAL DERIVATIVES AND THEIR APPLICATIONS 4 aaaaa 41 INTRODUCTON FUNCTIONS OF SEVERAL VARIABLES So far, we had discussed functions of a single real variable defined by y = f(x)Here in this chapter, we extend the concept of functions of two or more variables




Derivative Of Logₐx For Any Positive Base A 1 Video Khan Academy




If Log X 2 Y 2 Tan 1 Yx Then Prove That Dydx X Yx Y
Steps to use the derivative calculator Enter function you would like to differentiate and pay attention to the syntax checker tooltip which would inform you if the function is misspelled Enter differentiation variable if it is different from the default value Choose degree of differentiation Click 'Compute' buttonLogarithmic differentiation Calculator online with solution and steps Detailed step by step solutions to your Logarithmic differentiation problems online with our math solver and calculator Solved exercises of Logarithmic differentiation A partial derivative of a multivariable function is the rate of change of a variable while holding the other variables constant For a function z = f(x,y), we can take the partial derivative with respect to either x or y Partial




If U Log X 2 Y 2 Z 2 Then X 2u Y Z Y 2u Z X Z 2u X Y



What Is The Derivative Of X Y Y X 11 Quora
07 Second order partial derivatives Again, let z = f(x;y) be a function of x and y † @ 2z @x2 means the second derivative with respect to x holding y constant † @ 2z @y2 means the second derivative with respect to y holding x constant † @ 2z @x@y means difierentiate flrst with respect to y and then with respect to x The \mixed 2 I am new to partial derivatives and they seem pretty easy, but I am having trouble with this one ∂ ∂ x ln ( x 2 y 2) now if this was just d d x ln ( x 2) we would get 2 x xPartial Derivatives, Thomas Calculus 12 George B Thomas, Jr Maurice D Weir, Joel Hass All the textbook answers and stepbystep explanations




What Is The Derivative Of Log Y With Respect To X Mathematics Stack Exchange



What Is The Nth Derivative Of Logx Quora
Derivative of y = ln u (where u is a function of x) Unfortunately, we can only use the logarithm laws to help us in a limited number of logarithm differentiation question types Most often, we need to find the derivative of a logarithm of some function of xFor example, we may need to find the derivative of y = 2 ln (3x 2 − 1) We need the following formula to solve such problems For the y derivative of x^y Let x = k, a constant texf(y) = k^y/tex Natural log of both sides gives texln(f(y)) = ln(k^y)/tex texln(f(y)) = yln(k)/tex Differentiating texf'(y)/f(y) = ln(k)/tex texf'(y) = f(y)ln(k)/tex Since texf(y) = k^y/tex, you now have texf'(y) = ln(k)k^y/tex Substituting for x texf_y = ln(x)x^y/tex Q1458 A plane perpendicular to the x \)y\) plane contains the point (3, 2, 2) on the paraboloid 36z = 4x2 9y2 The crosssection of the paraboloid created by this plane has slope 0 at this point Find an equation of the plane (answer) Q1459 Suppose the temperature at (x, y, z) is given by T = xy sin(yz)




14 2 Limits And Continuity




Natural Logarithm Wikipedia
Derivative Of X 2 Y 2 Log Xy Youtube For more information and source, see on this link https//wwwyoutubecom/watch?v=kK2UW4FYL5gGet answer Find the partial derivatives of the functions at the indicated point G (x,y) = e ^(x3y) log (x ^(2) y ^(2)), (1, 1)Examples \frac {\partial} {\partial x} (\sin (x^2y^2)) \frac {\partial} {\partial y} (\sin (x^2y^2)) \frac {\partial} {\partial y\partial x} (\sin (x^2y^2)) \frac {\partial} {\partial w} (te^ { (\frac {w} {t})}) \frac {\partial} {\partial t} (te^ { (\frac {w} {t})}) \frac {\partial} {\partial v} (\sqrt {u^2v^2})
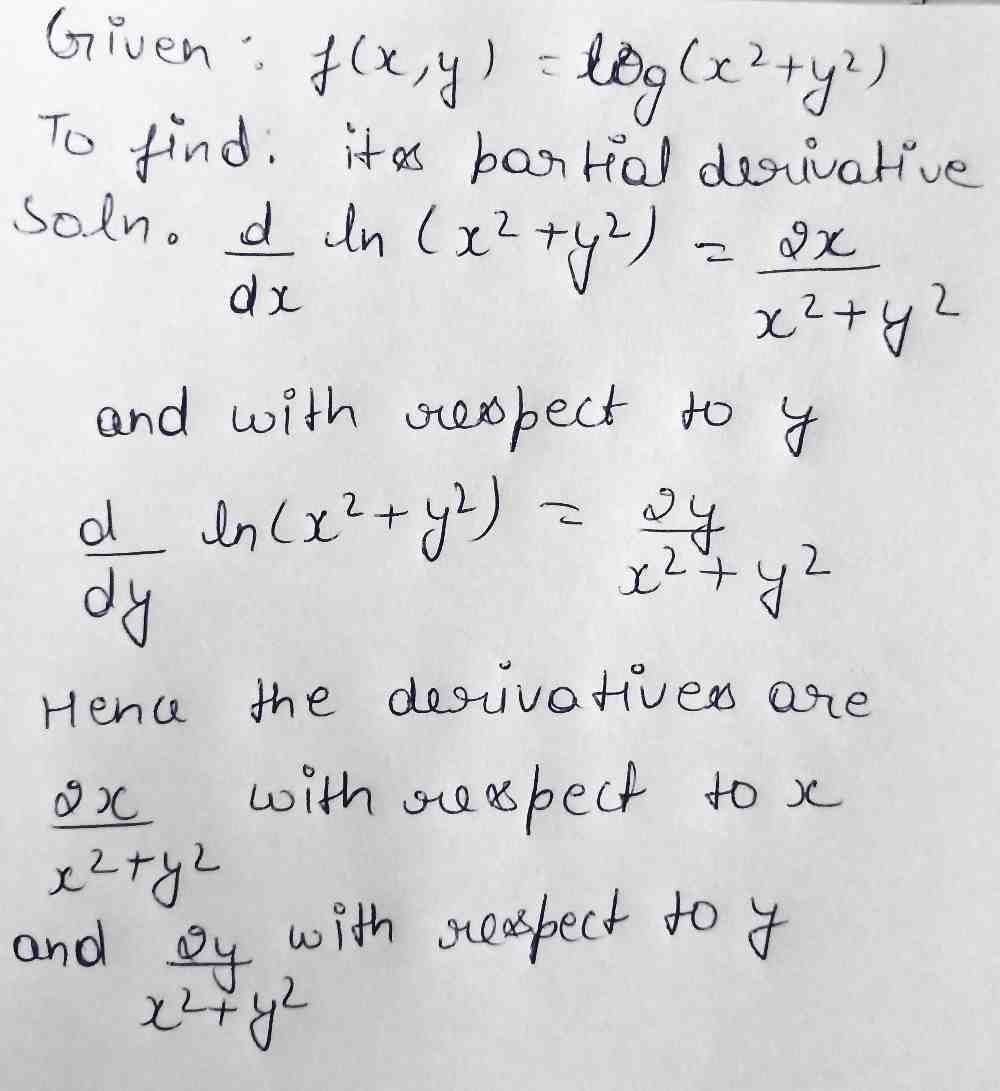



Partial Derivative Of Fx Y Ln X2 Y2 Gauthmath




Solved 2 3 Marks Consider The Function F X Y Log Chegg Com
Second regarding partial second derivatives You have for $(x,y)\neq(0,0)$ $$\begin{cases} \frac{\partial f}{\partial x}(x,y) = \frac{(x^2y^2)(3x^2yy^3)2x^2y(y^2x^2)}{(x^2y^2)^2}\\ \frac{\partial f}{\partial y}(x,y) = \frac{(x^2y^2)(x^33x y^2)2xy^2(y^2x^2)}{(x^2y^2)^2} \end{cases}$$Exactly analogous way a function of three variables f(x,y,u) has three partial derivatives ∂f ∂x, ∂f ∂y and ∂f ∂u, and so on for functions of more than three variables Each partial derivative is obtained in the same way as stated in Key Point 3 Key Point 3 The Partial DerivativesGeneralizing the second derivative Consider a function with a twodimensional input, such as Its partial derivatives and take in that same twodimensional input Therefore, we could also take the partial derivatives of the partial derivatives These are called second partial derivatives, and the notation is analogous to the notation for




5 Derivative Of The Logarithmic Function
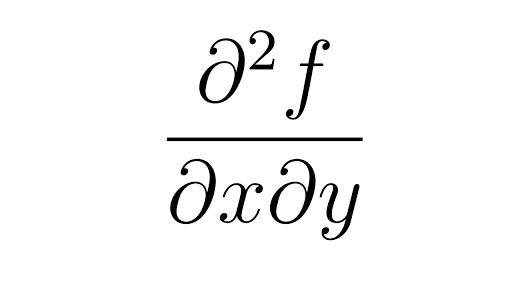



Second Partial Derivatives Article Khan Academy
Let's first think about a function of one variable (x) f(x) = x 2 We can find its derivative using the Power Rule f'(x) = 2x But what about a function of two variables (x and y) f(x, y) = x 2 y 3 We can find its partial derivative with respect to x when we treat y as a constant (imagine y is a number like 7 or something) f' x = 2x 0 = 2xDerivative Of X 2 Y 2 Log Xy Youtube For more information and source, see on this link Consider The Function F X Y Ln X 2 Y 2 3 Compute The Partial Derivatives Of The First And Second Order Mathematics Stack Exchange For more information and source, see on this linkPartial Derivative MCQ's Assignement QUESTION BANK Topic Partial Differentiation & Applications Q1If z = f ( x ay) g ( x – ay), then A zxx = zyy B zxx = a2 zyy C zyy = a2 zxx D zxx a2 zyy = 0 x tan−1 Q2 If x=log ¿ y), then fxy is equal to −1 A x 2




In Each Case Following Find The Partial Derivatives Chegg Com




Derivative Of Logarithm For Any Base Old Video Khan Academy
Partial Derivatives, University Calculus Early Transcendentals 4th Joel Hass, Christopher Heil, Przemyslaw Bogacki All the textbook answers and stepbystPartial Derivative Formulas and Identities There are some identities for partial derivatives as per the definition of the function 1 If u = f (x,y) and both x and y are differentiable of t ie x = g (t) and y = h (t), then the term differentiation becomes total differentiation 2If u = f (x,y) 2 then, partial derivative of u with respect to x and y defined as u x = n f ( x, y) n – 1 u_ {x} = n\left f\left ( x,y \right ) \right ^ {n – 1} ux = nf (x,y)n–1 ∂ f ∂ x \frac {\partial f} {\partial x} ∂x∂f
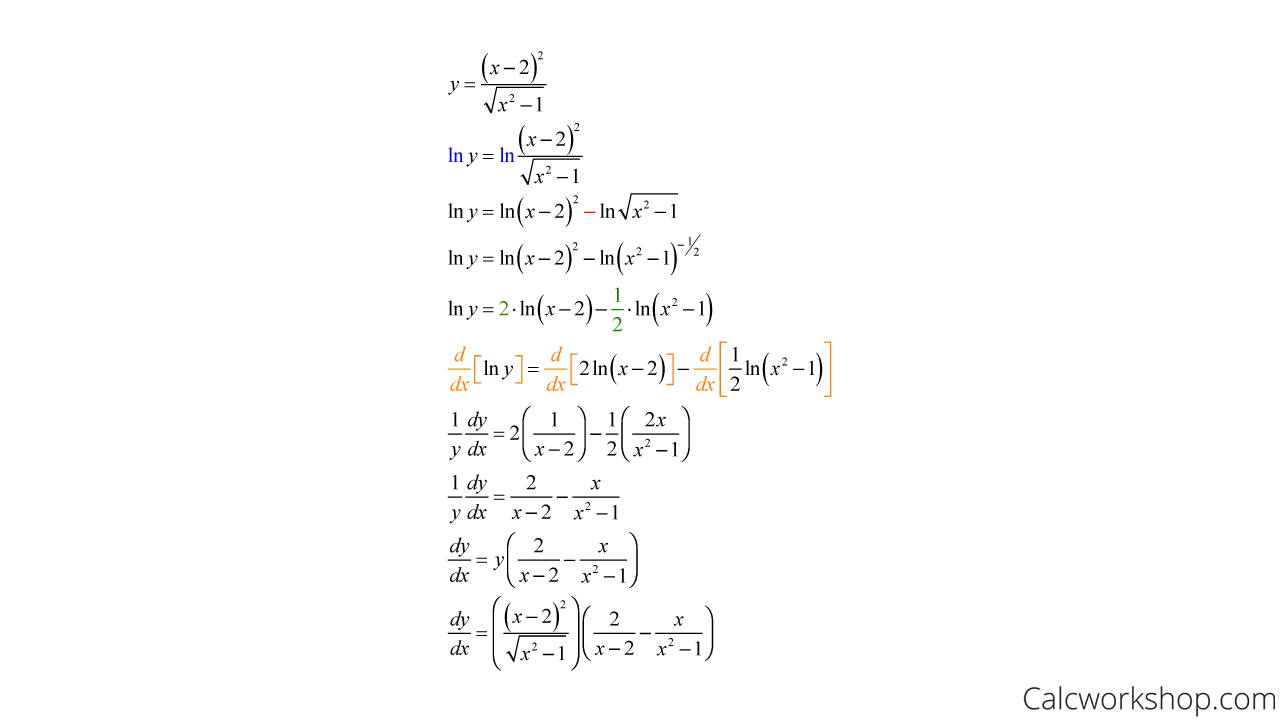



Logarithmic Differentiation W 7 Step By Step Examples



2
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more The first equation simplifies to \(x^2y^2=5\) and the second equation simplifies to \(x^2y^2=8\) The \(x\)intercept of the first circle is \((\sqrt{5},0)\) and the \(x\)intercept of the second circle is \((2\sqrt{2},0)\) There's a factor of 2 missing in all your second derivatives The result is exactly as you'd expect The variable you're differentiating with respect to, matters If it's x, then y is treated as a constant, and vice versa So if the "active" variable is leading in the numerator in one derivative, the same should apply in the other



5 Derivative Of The Logarithmic Function



If U Log X 2 Y 2 Xy Then X U X Y U Y Is A 0 B U C 2u Sarthaks Econnect Largest Online Education Community
Basic partial derivatives u = log( $x^2$ $y^2$ ), prove $ \frac{\partial^2 \;A critical point of a function with two variables is a point where the partial derivatives of first order are equal to zero The partial derivative of f(x,y) with respect to x is 2x sin(x^2y^2) This will be zero if x=0 or if sin(x^2y^2)=0 TheA second order partial derivative is simply a partial derivative taken to a second order with respect to the variable you are differentiating to As an example, let's say we want to take the partial derivative of the function, f(x)= x 3 y 5, with respect to x, to the 2nd order This is represented by ∂ 2 f/∂x 2
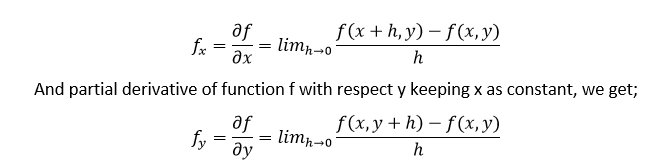



Partial Derivative Definition Formulas And Examples Partial Differentiation




Find All The First Order Partial Derivatives For The Chegg Com
U}{\partial x \partial y} \;About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us CreatorsCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history
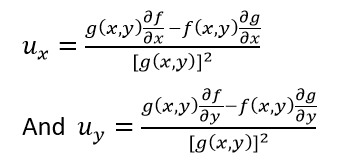



Partial Derivative Definition Formulas And Examples Partial Differentiation



Search Q Derivative Rules Tbm Isch
Partial Derivatives, Thomas Calculus 12 George B Thomas, Jr Maurice D Weir, Joel Hass All the textbook answers and stepbystep explanationsFind the partial derivatives of the following functions at the indicated points `"G"(x, y) = "e"^(x 3y) log(x^2 y^2), ( 1, 1)`Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history




If U Log X 2 Y 2 Z 2 Then Prove That X 2 Y 2 Z 2 D 2u Dx 2 D 2u Dy 2 D 2u Dz 2 1




Partial Derivative Examples Math Insight
Definition of Partial Derivatives Let f(x,y) be a function with two variables If we keep y constant and differentiate f (assuming f is differentiable) with respect to the variable x, using the rules and formulas of differentiation, we obtain what is called the partial derivative of f with respect to x which is denoted by Similarly If we keep x constant and differentiate f (assuming f is To find d/dx(sqrt(x^2y^2)), as part of an implicit differentiation problem, use the chain rule d/dx(sqrtx) = 1/(2sqrtx), so d/dx(sqrtu) = 1/(2sqrtu) (du)/dx d/dx(sqrt(x^2y^2)) = 1/(2sqrt(x^2y^2)) * d/dx(x^2y^2) = 1/(2sqrt(x^2y^2))(2x2y dy/dx) =1/(2sqrt(x^2y^2))2x 1/(2sqrt(x^2y^2))2y dy/dx =x/sqrt(x^2y^2) y/sqrt(x^2y^2) dy/dx In order to solve for dy/dx you will, of course, need the rest of the derivative ofAnswer to w = 7e^{xy} \log(x^{2} y^{2}) Find the partial derivatives \frac{\partial w}{\partial x} and \frac{\partial w}{\partial y} By signing




Compute The Partial Derivatives Of F X Y Log U Chegg Com




Show That Z Ln X 2 Y 2 2 Tan 1 Y X Satisfies The Laplaces S Equation Mathematics Stack Exchange




Solved Ex1 A Calculate Partial Derivatives 18 Si Z L Chegg Com
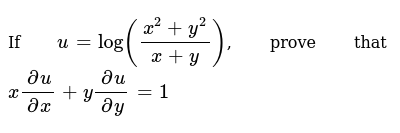



If U Log X 2 Y 2 X Y Prove That X Delu Delx Y Delu D




Derivative Of X 2 Y 2 Log Xy Youtube




Partial Derivative Examples Math Insight



1




Rd Sharma Class 12 Maths Solutions Chapter 11 Differentiation




21 Partial Derivatives Problem 4 Most Important Problem Partial Differentiation Youtube
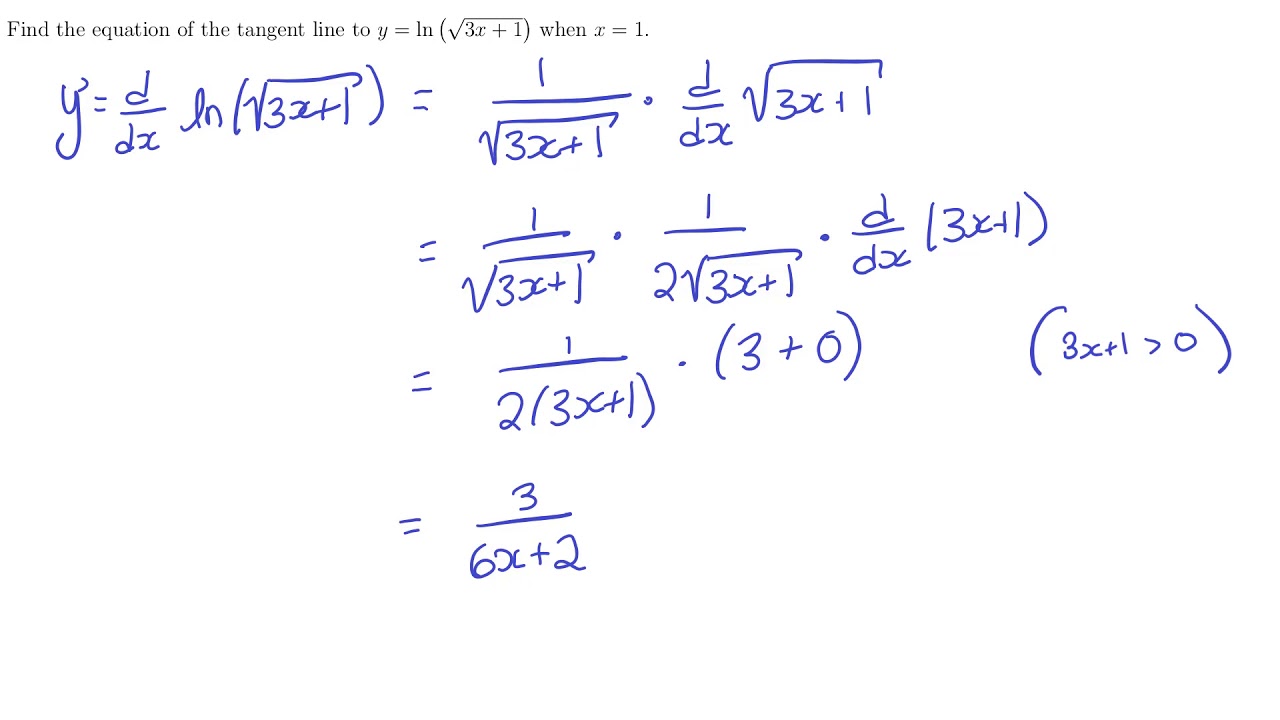



Derivatives Of Exponential Logarithmic Functions




Solved 1 Use L Hopital S Rale To Derive The Following Li Chegg Com




Mathematics Ii Tranquileducation




Ex 5 7 10 Find Second Order Derivatives Of Sin Log X



What Is The Second Derivative Of Y Log X 2 E X Quora




If Logsqrt X 2 Y 2 Tan 1 Y X Then Dy Dx Is




Implicit And Logarithmic Differentiation




1 The Following Questions Are Unrelated A Using Chegg Com




Pdf Functions Of Several Variables And Partial Di Erentiation 1 Functions Of Several Variables Mic Mus Academia Edu




Finding The Derivative Of Log X Video Lesson Transcript Study Com




Finding The Derivative Of Log X Video Lesson Transcript Study Com



If X Y E X Y What Is Dy Dx Quora



2
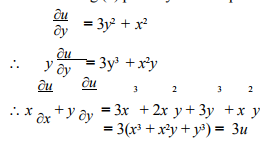



Partial Derivatives Differentiation Business Mathematics Statistics B Com Notes Edurev




Find All The Second Order Partial Derivatives Of The Chegg Com



2
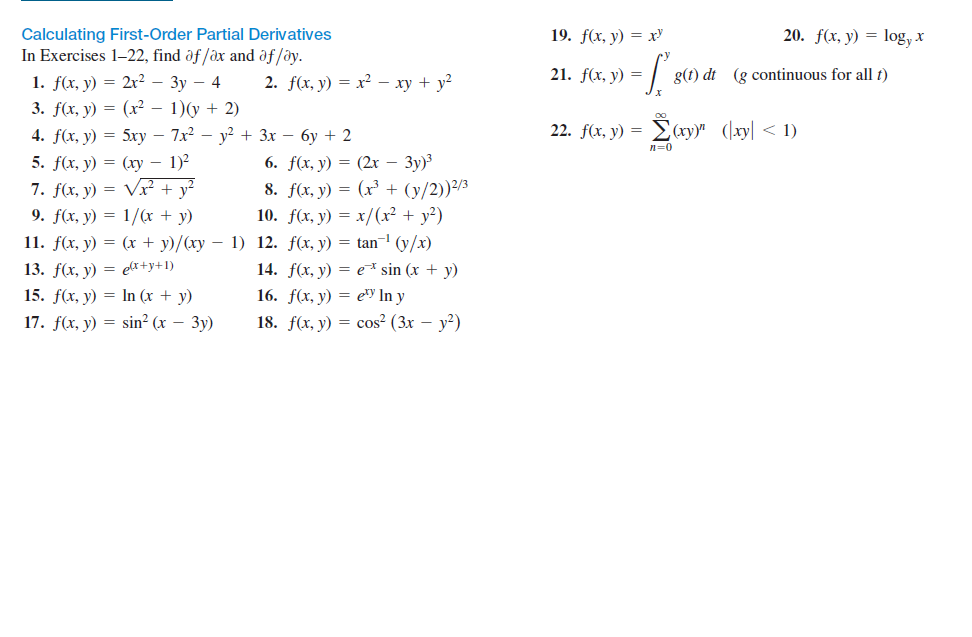



Answered Calculating First Order Partial Bartleby



How To Differentiate Y Xlogx Quora




Asgscv Partial Differential Equation Rates




Derivative Rules




If Log X2 Y2 2tan 1 Y X Then Show That Dy Dx X Y X Y Brainly In




Derivative Of Log Log X 2 With Respect To X Is



3



If X Y Y X What Is Dy Dx Quora




Eulers Partial Derivative If U Log X 4 Y 4 X Y Prove Xәu әx Yәu әy 3 Youtube



5 Derivative Of The Logarithmic Function




Derivative Of Log Confusion Mathematics Stack Exchange




If Y Log Tan X 2 Find Dy Dx



2




Find The Partial Derivative Of F X Y E X2 Y2 With Chegg Com




Ex 5 7 9 Find Second Order Derivatives Of Log Log X



2




Natural Logarithm Wikipedia




Finding The Derivative Of Log X Video Lesson Transcript Study Com




First Order Partial Derivatives Of F X Y Ln X 4 Y 4 Youtube



Could You Differentiate Sin Y Ln X X 2sin Y Wrt X And Explain Why The Derivative Of 2sin Y Becomes 0 Quora



Partial Derivative Of F X Y Xy X 2 Y 2 With Quotient Rule Youtube




For Any Function F X Y The First Partial Derivatives Are Represented By F F Fx And Fy X Y For Example If F X Y Log X Sin Ppt Video
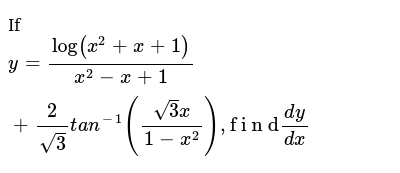



If Y Log X 2 X 1 X 2 X 1 2 Sqrt 3 T A N 1 Sqrt 3 X 1 X



What Is The Derivative Of E Logx Quora



What S The Partial Derivative Of F X Y Log To The Base X Y Quora



17 5 Higher Order Partial Derivatives Graphing Calculator By Mathlab User Manual
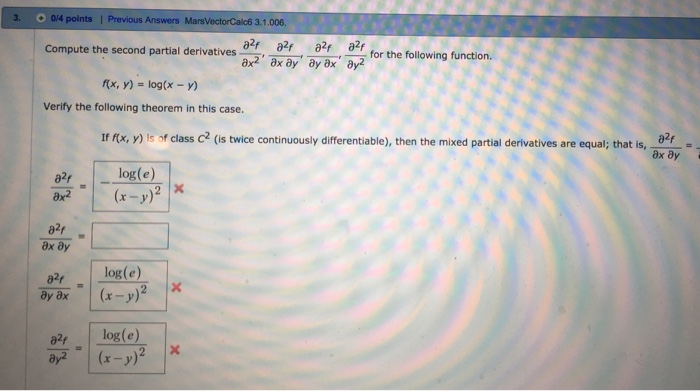



Solved Compute The Second Partial Derivatives Partial Dif Chegg Com



Rules Of Calculus Multivariate




Derivative Of Log Confusion Mathematics Stack Exchange
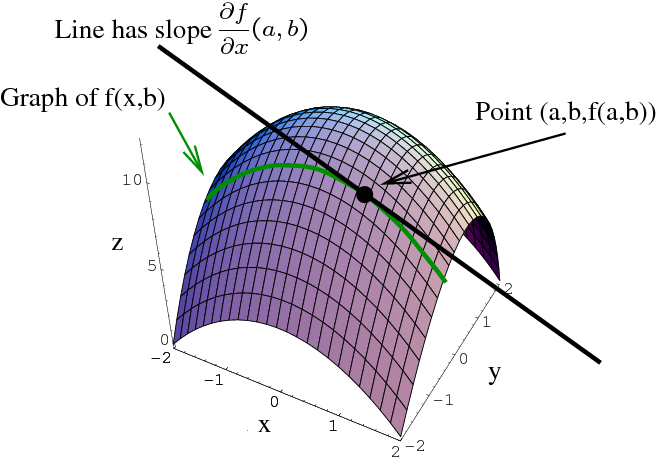



Partial Derivative By Limit Definition Math Insight
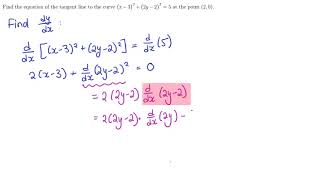



Implicit And Logarithmic Differentiation




Ex 5 7 4 Find Second Order Derivatives Of Log X Teachoo



Finding The Derivative Of Log X Video Lesson Transcript Study Com




Find Second Derivative Of Log X Calculus Youtube




Derivative Of Log Y Mathematics Stack Exchange




If Y Log X 2 X 1 X 2 X 1 2 Sqrt 3 T A N 1 Sqrt 3 X 1 X




8 Find All Second Order Partial Derivatives For The Chegg Com




Learn How To Find The First Order Partial Derivatives Of F X Y Ln Xy 3 With Log Properties Youtube




Differentiate Log X 2 Sqrt X 2 4x 1 With Respect To X



1




Consider The Function F X Y Ln X 2 Y 2 3 Compute The Partial Derivatives Of The First And Second Order Mathematics Stack Exchange




Part 4 4 Logarithmic Function Log Ax Derivative Of Exponential Logarithmic Functions Youtube




If U Log X 2 Y 2 Z 2 Verify 2u X Y 2u X Y




Solved Find Partial Differential F Partial Differential X Chegg Com




Derivative Calculator Wolfram Alpha



5 Derivative Of The Logarithmic Function




Doc Chapter Four Derivatives Of Multivariate Functions Partial Differentiation Habtamu Destaw Academia Edu
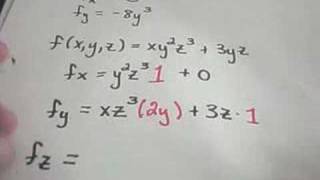



Finding Partial Derviatives Youtube
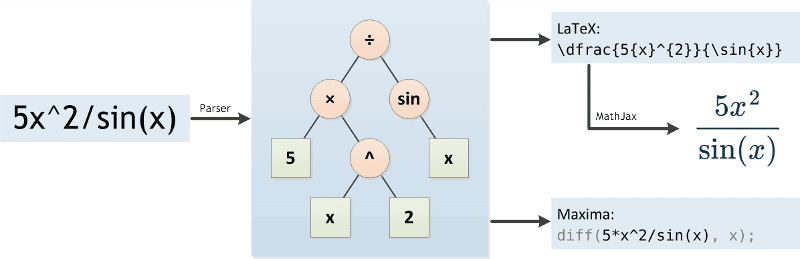



Derivative Calculator With Steps



What Is The Nth Derivative Of Logx Quora




Log X Y 2xy Detailed Login Instructions Loginnote




Implicit Differentiation Advanced Example Video Khan Academy




21 Partial Derivatives Problem 4 Most Important Problem Partial Differentiation Youtube
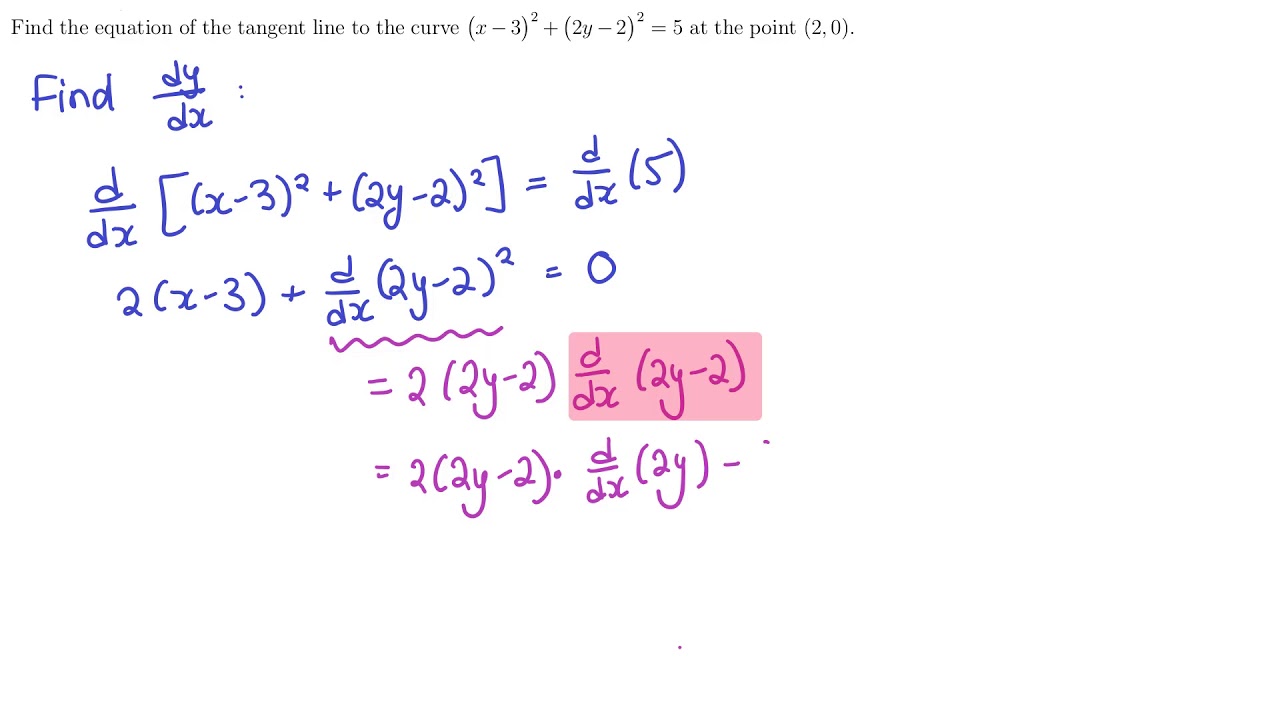



Implicit And Logarithmic Differentiation
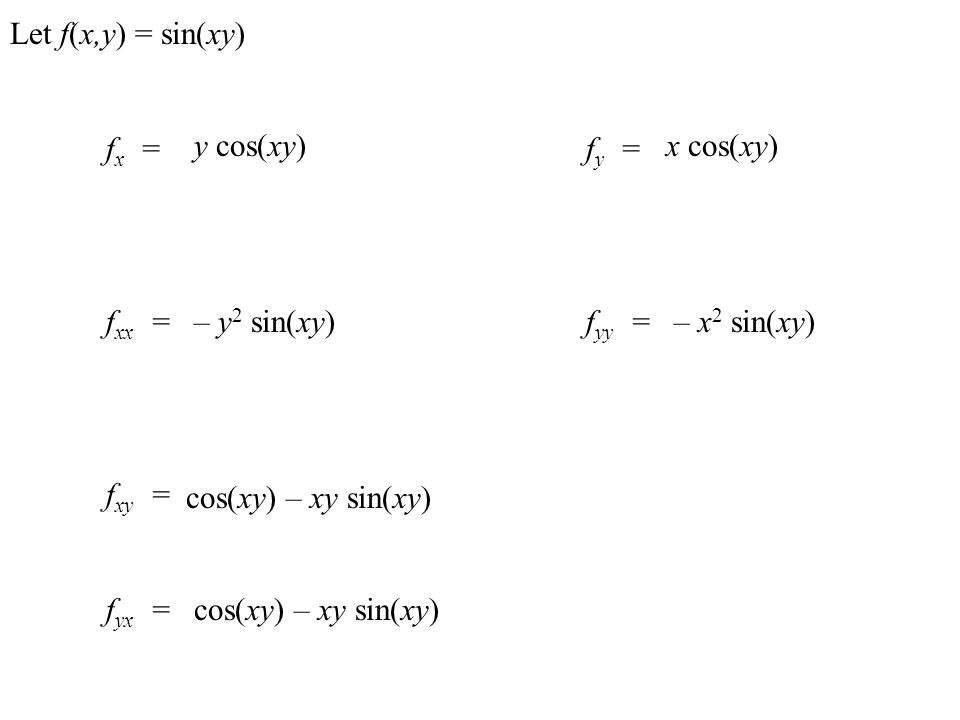



For Any Function F X Y The First Partial Derivatives Are Represented By F F Fx And Fy X Y For Example If F X Y Log X Sin Ppt Video



0 件のコメント:
コメントを投稿